
|
... mehr dazu: Das Dodekaeder: ein Würfel mit 6 Dächern Diese Konstruktion des Dodekaeders aus dem Würfel stammt von Euklid. Er beschreibt sie in seinen »Elementen« in Buch XIII, §17. Die Konstruktion ist nur möglich, weil ein Dodekaeder doppelt so viele Flächen hat wie ein Würfel. Und sie kann auch nur mit Walmdächern funktionieren: Die entstehen aus einem Satteldach, wenn man jeden Giebel (senkrechtes Dreieck) durch einen »Walm« (schräges Dreieck) ersetzt. Wie die Animation zeigt, besteht jedes Dach als geschlossener Körper aus 5 Flächen: Seine Grundfläche ist ein Quadrat von den Maßen der Würfelflächen. Die restlichen Flächen sind die 4 Einzelteile, die wir erhalten, wenn wir zwei regelmäßige Fünfecke jeweils entlang einer Diagonale in ein gleichschenkliges Trapez und ein gleichschenkliges Dreieck zerlegen. Das Dachnetz konstruieren wir, indem wir an die vier Seiten des Würfel-Quadrats die 4 Einzelteile anlegen, und zwar so, dass Trapeze und Dreiecke jeweils der gleichen Form gegenüber liegen. Damit das passt, müssen Würfelkanten und Fünfeckdiagonalen natürlich dieselbe Länge haben.
In der Sprache der Zimmerleute: Die beiden Trapeze bilden die »Traufseiten« jedes Würfeldachs, die beiden Dreiecke die »Walme«. Die Traufseiten des Dachs schließen sich mit je einem Walm zweier Nachbardächer zu zwei regelmäßigen Fünfecken zusammen. Aus 6 Quadraten werden so 12 Fünfecke, aus dem Würfel entsteht ein Dodekaeder. Da im regelmäßigen Fünfeck Diagonalen- und Seitenlänge im Goldenen Schnitt stehen, gilt das auch für die Kantenlängen von Würfel und Dodekaeder. Verwenden wir die Verhältniszahl des Goldenen Schnitts, die sogenannte »Goldene Zahl«
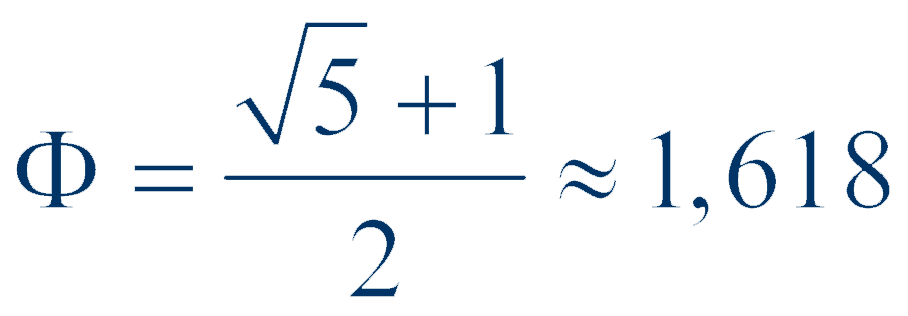 so ist hier die Kantenlänge des Würfels also genau die Φ-fache Kantenlänge des Dodekaeders.
Allerdings: Dass diese Konstruktion wirklich funktioniert, ist damit noch längst nicht erklärt. Was wir bisher überlegt haben, sind nur notwendige Voraussetzungen, die erfüllt sein müssen, wenn das alles überhaupt klappen soll. Wir müssten beweisen, dass sie auch hinreichend sind, damit wirklich ein Dodekaeder entsteht. Denn Walme und Traufseiten müssen ja genau im richtigen Winkel geneigt sein, damit Trapez und Dreieck in einer Ebene liegen. Sonst hätten die Fünfecke an einer Diagonale einen Knick, und statt eines Dodekaeders aus 12 Fünfecken hätten wir ein »Ikositetraeder« (24-Flächner) aus 12 Dreiecken und 12 Trapezen. Der Beweis, dass tatsächlich ebene Fünfecke entstehen, ist allerdings etwas aufwendig und »formellastig«, so dass wir an dieser Stelle darauf verzichten. Dass 8 der Dodekaeder-Ecken stets einen Würfel bilden, lässt sich unmittelbar an ihren Koordinaten ablesen. Die platonischen Körper sind die regelmäßigsten aller Polyeder. Diese maximale Symmetrie wird (außer beim Würfel) wesentlich durch den Goldenen Schnitt bestimmt. Daher taucht bei den Koordinaten von Tetra-, Okta-, Dodeka- und Ikosaeder die Goldene Zahl wieder auf. Bringt man ein Dodekaeder in ein räumliches Koordinatensystem, richtet man es darin geschickt aus und passt seine Größe an, so haben seine 20 Ecken folgende Koordinaten: Die erste Klammer repräsentiert 8 Ecken, die drei übrigen jeweils 4 Ecken. Die 8 Ecken der ersten Klammer bilden die Ecken eines Würfels der Kantenlänge 2. Dies ist der blaue Würfel oben in unserer Konstruktion. Das Ikosaeder: 3 goldene Rechtecke Für das Ikosaeder gibt es eine ähnliche Konstruktion wie für das Dodekaeder. Auch sie können wir unmittelbar an den Koordinaten ablesen. Die 12 Ikosaeder-Ecken haben die Koordinaten: Jede der drei Klammern repräsentiert jeweils vier Ecken, die in einer gemeinsamen Koordinatenebene liegen, da bei allen vier dieselbe Koordinate den Wert 0 hat: Die Ecken der linken Klammer liegen in der x-z-Ebene, die der mittleren in der y-z-Ebene, die der rechten in der x-y-Ebene. In allen drei Ebenen bilden die vier Ecken Rechtecke, und zwar besondere: Da die Seitenlängen jeweils 2 bzw. 2Φ betragen, sind alle Rechtecke kongruent, und ihre Seiten stehen im Verhältnis des Goldenen Schnitts (längere zu kürzere wie Φ zu 1). Die drei Rechtecke sind demnach kongruente »Goldene Rechtecke«.
Das hat eine unmittelbare konstruktive Bedeutung: Man kann ein Ikosaeder konstruieren, indem man drei Goldene Rechtecke gleicher Größe so symmetrisch wie möglich ineinander steckt. Die Ecken der Rechtecke spannen dann ein Ikosaeder auf. Handwerklich ist dieses Ineinanderstecken allerdings nicht ganz einfach und erfordert den geschickten Gebrauch einer Schere. Braucht man auch Klebstoff? Oder lassen sich die drei Rechtecke allein durch Einschnitte, bei denen also keines ganz durchtrennt wird, zusammenstecken? Probieren Sie es aus. |

